密码学中的零知识证明技术在web3世界中有着广泛的应用,包括隐私计算、zkRollup等。其中,Layer2项目FOX中使用的FOAKS是一种零知识证明算法。在上述系列应用中,有两个属性对于零知识证明算法极其重要,那就是算法的效率和交互性。
算法效率的重要性不言而喻。一个高效的算法可以明显降低系统运行时间,从而降低客户端延迟,显著提升用户体验和效率,这也是FOAKS致力于实现线性证明时间的重要原因。
另一方面,从密码学的角度来看,零知识证明系统的设计往往依赖于证明者和验证者之间的多轮交互。比如很多介绍零知识证明的科普文章中使用的“零知识洞穴”的故事,证明的实现依赖于阿里巴巴(证明者)和记者(验证者)多轮的信息传递和互动。但实际上,在很多应用场景下,依赖交互会让系统不再可用,或者极度增加延迟。就像在zkRollup系统中,我们期望证明者(也就是FOX中的文件夹)在本地计算出正确的证明值,而不依赖于与验证者的交互。
从这个角度来看,如何将交互式零知识证明协议转化为非交互式的是一个非常有意义的问题。在本文中,我们将介绍FOX使用经典的Fiat-Shamir启发式算法在Brakedown中生成挑战以实现非交互式协议的过程。
挑战零知识证明算法在零知识证明中已经得到了极其普及的应用。近年来,包括FOAKS、Orion、zk-stark在内的各种算法也相继诞生。这些算法,以及密码学中早期sigma协议的核心证明逻辑,都是证明者先向验证者发送某个值,验证者通过本地随机数生成一个挑战,并将随机生成的挑战值发送给证明者。证明者需要真实的知识来做出以高概率通过验证者的响应。比如零知识的山洞里,一个记者扔硬币告诉阿里巴巴是从左边出来还是从右边出来。这里的“左右”是对阿里巴巴的挑战。如果他真的会法术,绝对可以从要求的方向走出来,否则有一半的几率会失败。
这里,我们注意到挑战的产生是一个关键步骤,它有两个要求,随机的和不可预测的。首先,随机性保证了它的概率性。第二,如果证明者可以预测挑战值,就意味着协议的安全性被破坏,证明者可以在不知情的情况下通过验证,类比可以继续。如果阿里巴巴能预测到记者让他从哪边出来,他甚至不用咒语就能提前进入那一边,结果显示他也能通过协议。
所以我们需要一种方法,让证明者在本地生成这样一个不可预测的随机数,同时可以被验证者验证,这样就可以实现一个非交互式的协议。
哈希函数(Hash Function)哈希函数的名字我们可能并不陌生。无论是比特币共识协议POW中挖掘的数学问题,还是压缩数据量、构造消息验证码等。,有哈希函数。在上面提到的不同协议中,实际使用了哈希函数的不同属性。
具体来说,安全哈希函数的属性包括以下内容:
可压缩性:确定的哈希函数可以将任意长度的消息压缩到固定长度。
有效性:给定输入X,很容易计算输出h(x)。
防碰撞:给定一个输入x1,很难找到另一个输入x2,x1x2,h(x1)= h(x2)。
注意,哈希函数如果满足防碰撞,就必须满足一个方向,即给定一个输出y,很难找出x满足h (x) = y,在密码学中,理论上不可能构造出绝对满足单向的函数,但哈希函数在实际应用中基本可以看作单向函数。
这样我们就可以发现,上述应用对应了哈希函数的几种不同性质,同时我们说哈希函数还有一个非常重要的提供随机性的功能。虽然目前还无法构造出密码学理论中所需要的完美随机数生成器,但是实际中哈希函数也可以起到这个作用,这为我们后面要介绍的Fiat-Shamir启发式的技巧提供了基础。
Fiat-Shamir启发式其实Fiat-Shamir启发式就是用hash函数对之前生成的脚本进行hash得到一个值,并将这个值作为挑战值。
因为散列函数H被认为是一个随机函数,所以挑战是均匀随机选择的,与证明者的信息和承诺无关。安全分析认为爱丽丝无法预测H的输出,只能将其视为神谕。在这种情况下,爱丽丝在不遵守协议的情况下(尤其是在她不知道必要秘密的情况下)做出正确反应的概率与h的范围大小成反比。
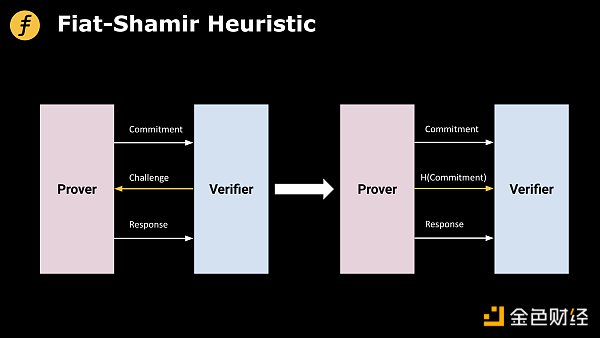
图1:使用Fiat-Shamir启发式算法实现非交互式证明
在本节中,我们展示了Fiat-Shamir启发式算法在FOAKS协议中的应用,主要用于生成Brakedown部分的挑战,从而实现非交互式FOAKS。
首先,我们看到在Brakedown生成证明的过程中,需要挑战的步骤是“邻近测试”和Merkle树的证明部分(读者可以参考之前的文章《FOAKS中了解多项式承诺协议Brakedown》)。对于第一点,原来的流程是证明者需要一个这里验证者生成的随机向量,计算过程如下图所示:

图2:非交互验证FOAKS中的Brakedown检查
现在我们使用散列函数让证明者自己生成这个随机向量。
设γ0=H(C1,R,r0,r1)。相应的,验证者的验证计算中也需要这一步计算γ0。根据这种结构可以发现,证明者在生成承诺之前不能* * *挑战值,因此不能根据挑战值提前“作弊”,即相应生成一个虚假的承诺值。同时根据哈希函数输出的随机性,这个挑战值也满足随机性。
对于第二点,设= h (c1,r,r0,r1,c1,y1,cγ 0,yγ 0)。
在改进的非交互式Brakedown多项式承诺中,我们使用伪代码给出证明和验证函数,这也是FOAKS系统中使用的函数。
功能PC。Commit(ϕ):
Parse是一个k × k矩阵。证明者在本地计算编码C1、C2、C1的张量码是k × n矩阵,C2是n × n矩阵。
对我来说
一致性:
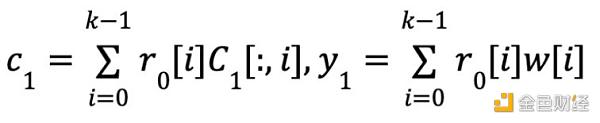
证明者将c1,y1,cγ0,yγ0发送给验证者。
证明者计算一个向量作为挑战,其中φ= H(C1,R,r0,r1,C1,y1,cγ0,yγ0)
对于idx∈do
证明者将C1 [:,idx]和C2 [:,idx]的根idx的Merkle树证明发送给验证者
功能PC。verify _ eval(πx,x,y= ϕ (X),r)
邻近度:∀idx ∈,Cγ0 [idx] ==
并且Ec(yγ0) == Cγ0
一致性:∀idx ∈,C1 [idx] ==
并且Ec(y1) == C1
y==1,y1 & gt
∀idx ∈,Ec ( C1[:,idx])与ROOTidx一致,ROOTidx的Merkle树证明有效。
如果上述所有条件都成立,则输出接受。否则输出拒绝。
结论很多零知识证明算法在设计之初就依赖于证明者和验证者之间的交互,但这种交互证明协议并不适合追求高效率、网络通信开销大的应用场景,比如链上数据隐私保护、zkRollup等。通过Fiat-Shamir启发式算法,证明者可以在不破坏协议安全性的情况下在本地生成一个随机数“挑战”,并且可以被证明者验证。根据该方法,FOAKS还实现了非交互式证明,并将其应用于系统中。
参考文献1。菲亚特、阿莫斯;阿迪·沙米尔(1987年)。“如何证明自己:识别和签名问题的实用解决方案& # 8221;。密码学进展—密码& # 8217;86.计算机科学讲义。施普林格柏林海德堡。263: 186–194.doi:10.1007/3-540-47721-7_12。国际标准书号978-3-540-18047-0。
2 . https://www . cn blogs . com/zhuowangy2k/p/12246575 . html
执笔:福克斯科技CEO康水月;孟玄寂,福克斯科技公司首席科学家
来源:DeFi之路
温馨提示:注:内容来源均采集于互联网,不要轻信任何,后果自负,本站不承担任何责任。若本站收录的信息无意侵犯了贵司版权,请给我们来信(j7hr0a@163.com),我们会及时处理和回复。
原文地址"交互式零知识证明的缺点,交互式和非交互式区别":http://www.guoyinggangguan.com/qkl/176194.html。
微信扫描二维码关注官方微信
▲长按图片识别二维码




