Ronin 黑客计中计 听说过扭曲攻击漏洞吗？

作者:约翰

根据慢雾安全团队的信息，2023年3月13日，以太坊链条上的贷款项目欧拉金融遭到攻击，攻击者获利约2亿美元。

攻击欧拉后，黑客将100个ETH转给了从浪人那里窃取了超过6.25亿美元的黑客拉扎勒斯(Lazarus)，目的是为了混淆视听，避免追查。拉扎勒斯紧随其后，立即在链上向欧拉黑客发送了一条加密消息。

消息的内容是提示Euler开发者使用etheces。

但是这个漏洞的优势和难度是很难的，需要一个经常契合的场景来发动攻击。浪人剥削者有机会发动扭曲攻击吗？

ECDH算法是一种基于椭圆曲线加密的密钥交换算法。它类似于传统的Diffie-Hellman (DH)算法，但密钥交换是通过椭圆曲线上的数学运算实现的，安全性更高。

以下是ECDH算法的步骤:

1.椭圆曲线:在密钥交换之前，通信方需要选择一条椭圆曲线，该曲线必须填充一些数学特征，比如离散对数问题。

2.分为私钥和公钥:每次通信都需要一对私钥和公钥。私钥是一个随机数，用于计算公钥。公钥是一个点，在椭圆曲线上，用私钥计算。

3.公钥交换:通信伙伴将公钥发送给对方。

4.计算共享密钥:通信特使为发送的公钥和私钥计算共享密钥。这个共享密钥可以用来加密通信中的数据，确保通信的机密性。

为了描述爱丽丝和鲍勃分别代表上双，G是基点，假设:

爱丽丝的私钥是A，那么爱丽丝的公钥是A = aG；

鲍勃的私钥是B，那么鲍勃的公钥是B = bG。

核心知识点在共享密钥计算法。根据群的乘法和交换定律，他们只要得到对的公钥就可以计算出共享密钥:

S = aB = a(bG) = b(aG) = bA

如果Alice想窥探Bob的私钥，可以选择一个常数阶为Q的曲线点H(点数往往很少)(这个点不是任何特定私钥对应的公钥，只是Bob不知道)。因为群是循环群，当Bob计算S′= BH时，他的S′会在这几个点群内。Alice不知道Bob的私钥B，但是她可以通过穷举法得到X充满S' = xh，这种情况下B ≡ x mod Q .显然X是非常，最q的。

需要多少个扭转点？这取决于每次选择的阶数q，阶数乘法要求超过私钥的最大值，即满:

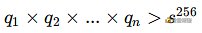
如果我每次都选择Q点，我需要和N交互的次数可以少一些，但是Q越多意味着越难穷尽，所以需要根据爱丽丝的计算性能来选择。

在事件结束时，我们分析了ECDH算法的风险和攻击原理。让我们回头看看图书馆的文献。事实上，它只制造了一个类似于ECDH的算法。它在构造共享私钥时使用一个临时密钥，根本不需要获取加密的私钥，所以不会对加密造成风险。

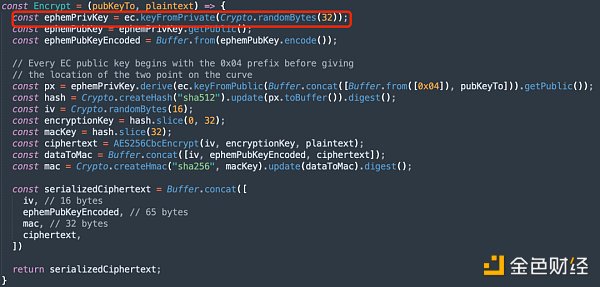
那么有没有可能Ronin Exploiter是在试图帮助社会科学指导Euler Exploiter制造其他有问题的设备呢？我们知道，PGP加密协议？

无独有偶，我们很快发现了广泛使用的开源库openpgpjs。

在故事的最后，我认为Ronin Exploiter使得低版本elliptic的漏洞秘密窃取Euler Exploiter的私钥成为可能。不，那个链上的消息可能真的是为了讨论。更进步的剧情需要更多的社会课程，但欧拉剥削者已经警醒。

我已经提到了扭转攻击的原理，但是在实际的实施过程中还有一个问题需要解决:

1.如何构造扭曲点？

2.当Bob共享密钥S & # 8217当消息被加密时，它不会发送S & # 8217传输给Alice，因为Bob认为Alice根据协议已经知道了这个密钥，那么Alice如何获得S & # 8217然后呢。

例如，这条曲线25519，它的曲线路线是:

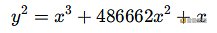
我们随意改变四个参数，得到一条新的曲线，比如:

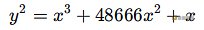
让Sagemath数学软件来表示)然后我们计算它的阶次并进行因式分解:

grp = e . abelian _ group()G = grp . gens()，

0] Gorder = G.order() print( "{0} = {1}".format(Gorder, factor(Gorder)) )

计算结果：

选择 19442993 这个⼤⼩适中的数，⽤中国剩余定理创建⼀个含有 19442993 个元素的⼦群：

19442993, Gorder//19442993]) P1 = x * G

到这⾥我们就得到了第⼀个扭曲的点，把它当作公钥发送给 Bob，Bob 就可以计算第⼀个共享密钥：

/image-10/[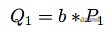

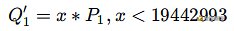
最终结果可以表示为:

私钥b可以通过中国的余数定理来计算:

x = crt([ x1，x2，x3，x4，x5，x6，x7，x8，x9]，[ 19442993，3645143，184879577，5110460161，15272631587，208137522259，64927105657，60824497，213156431])打印该漏洞虽有益于现场，但却是一个有价值的漏洞，希望对经济学家的学习和研究有所启发。

最后，感谢领先的数字资产托管服务提供商Safeheron提供的专业技术建议。

参考资料:

[1].https://ethers can . io/tx/0x cf0 b 3487 DC 443 f1 ef 92 B4 Fe 27 ff 7 f 89 e 07588 CDC 0 e 2 b 37d 50 ADB 8158 c 697 ce a6

[2].https://github.com/LimelabsTech/eth-ecies

[3].GitHub & # 8211open pgpjs/open pgpjs:JavaScript的OpenPGP实现

[4].椭圆曲线构造函数& # 8211；椭圆曲线

温馨提示：注：内容来源均采集于互联网，不要轻信任何，后果自负，本站不承担任何责任。若本站收录的信息无意侵犯了贵司版权，请给我们来信(j7hr0a@163.com)，我们会及时处理和回复。

原文地址"Ronin 黑客计中计 听说过扭曲攻击漏洞吗？"：http://www.guoyinggangguan.com/qkl/167441.html。

微信扫描二维码关注官方微信
▲长按图片识别二维码